[인프런 자바/java] 7. 조합의 경우수(메모이제이션) _디버깅의 눈물

조합식 nCr이 의미하는 것은 n개 중에서 중복없이 r개를 뽑는 모든 경우의 수를 구하는 것이다.
예시 1의 5C3을 예로, '5개 중에서 3개를 중복없이 뽑는 경우'를 구하려면,
1)5를 무조건 포함시키고 나머지 4개 중에서 2개를 뽑는 경우(4C2),
2)5를 무조건 배제하고, 나머지 4개 중에서 3개를 뽑는 경우(4C3)
이 두 가지 경우로 나눌 수 있다.
따라서 두 가지 경우의 합(4C2 + 4C3)이 5C3이 되는 것이다.
체크 포인트
1. DFS(깊이 우선 탐색) 사용
-모든 경우의 수를 구하는 문제이기 때문에 최단 값을 구하는 BFS 대신 DFS를 사용했다.
2. DP(Dynamic Programming, 동적 계획법)의 하나인 '메모이제이션' 방법을 사용
-DFS를 통해 모든 경우의 수를 확인하는 것으로 풀리는 문제들도 존재하지만, 경우의 수가 매우 큰 경우 시간초과 문제가 발생할 수도 있다.
-이 때 효율적으로 메모리를 줄여줄 수 있는 DP(Dynamic Programming, 동적 계획법)을 사용할 수 있다.
-대표적으로 메모이제이션 방법이 존재한다.
-나무위키 정의에 따르면, 메모이제이션이란,
"컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술"이다.
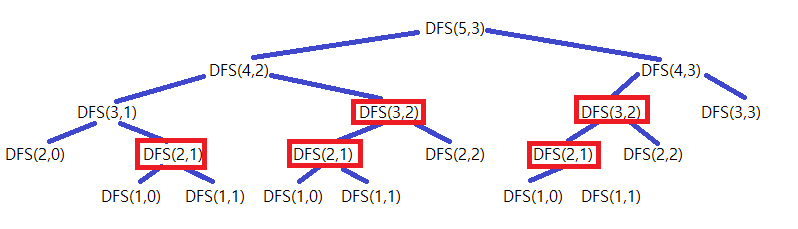
-위의 5C3 계산 과정을 보면,
DFS(5,3)-DFS(4,2)-DFS(3,1)-DFS(2,0)-DFS(2,1)-DFS(1,0)-DFS(1,1)-DFS(3,2)-DFS(2,1)-DFS(1,0)-DFS(1,1)-DFS(2,2)-DFS(4,3)-DFS(3,2)-DFS(2,1)...
의 순으로 탐색이 진행되면서 DFS(2,1), DFS(3,2)와 같은 중복 DFS 계산이 등장한다.
-메모이제이션을 이용한다면, 동일한 DFS 탐색이 등장할 때, 미리 저장해둔 값을 활용한다.
-결과적으로 동일한 DFS(2,1)을 중복계산하지 않고 결과를 효율적으로 도출할 수 있는 것이다.
static int DFS(int n, int r) {
// 해당 메모이제이션이 이미 존재하는 경우,
if(combi[n][r]>0){
// 존재하는 값 return
return combi[n][r];
}
// n==r : n개 중 n개를 뽑는 경우의 수는 오직 1개
// r==0 : n개 중 하나도 뽑지 않는 경우의 수는 오직 1개
if(n==r || r==0){
return 1;
}
// 이외의 경우,
else{
// 조합식 return
return combi[n][r] = DFS(n-1,r-1) + DFS(n-1,r);
}
} // end of DFS
-메모이제이션 과정은,
1) 중복되는 결과값을 저장해주는 2차원 배열 combi를 생성해,
2) DFS(2,1)과 같은 중복계산값을 combo[2][1]로 저장해두고,
3) DFS과정에서 combo[n][r]의 값이 0보다 크다면(계산한 값이 존재한다면), 해당 값을 return 시키도록 구현했다.
풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
// 조합 메모이제이션 배열
static int[][] combi;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
// 조합 n에 들어가는 자연수
int n = Integer.parseInt(st.nextToken());
// 조합 r에 들어가는 자연수
int r = Integer.parseInt(st.nextToken());
// 메모이제이션 배열 초기화
combi = new int[n+1][n+1];
//DFS 탐색 시작
System.out.println(DFS(n,r));
} // end of Main
static int DFS(int n, int r) {
// 해당 메모이제이션이 이미 존재하는 경우,
if(combi[n][r]>0){
// 존재하는 값 return
return combi[n][r];
}
// n==r : n개 중 n개를 뽑는 경우의 수는 오직 1개
// r==0 : n개 중 하나도 뽑지 않는 경우의 수는 오직 1개
if(n==r || r==0){
return 1;
}
// 이외의 경우,
else{
// 조합식 return
return combi[n][r] = DFS(n-1,r-1) + DFS(n-1,r);
}
} // end of DFS
} // end of Main